Topics in Theoretical Computer Science: Unlocking the Secrets of Computation and Information

Theoretical computer science is the study of the foundations of computing and information. It explores the fundamental concepts and principles that underlie the design, analysis, and applications of computer systems and software. This field provides a rigorous framework for understanding the limits and capabilities of computation, opening doors to technological advancements and scientific discoveries.
5 out of 5
| Language | : | English |
| File size | : | 14553 KB |
| Text-to-Speech | : | Enabled |
| Enhanced typesetting | : | Enabled |
| Screen Reader | : | Supported |
| Print length | : | 192 pages |
In this comprehensive guide, we will delve into the core topics of theoretical computer science, unraveling the intricate web of concepts that shape the digital landscape. From the abstract realm of automata theory to the practical applications of algorithms, we will explore the foundations that underpin the world of computation.
Automata Theory
Automata theory provides the mathematical framework for studying the behavior of abstract machines, known as automata. These theoretical models capture the essence of computational processes, enabling us to analyze their capabilities and limitations.
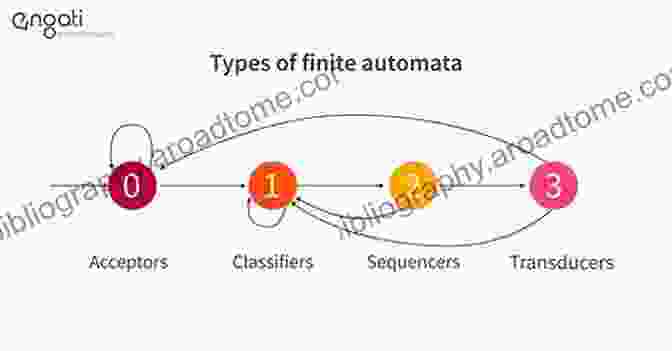
Finite Automata
Finite automata are simple machines that recognize regular languages, a class of languages with a regular structure. They consist of a finite number of states and transitions between states, and they operate by reading input symbols sequentially and changing states accordingly. Finite automata find applications in pattern matching, lexical analysis, and natural language processing.
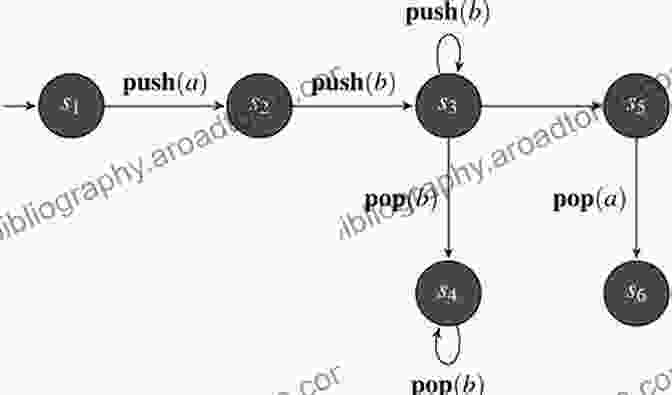
Pushdown Automata
Pushdown automata are more powerful than finite automata and can recognize context-free languages, a broader class of languages used in programming languages, compilers, and XML processing. They introduce the concept of a stack, which allows them to remember and retrieve information during computation, making them suitable for modeling complex syntactic structures.
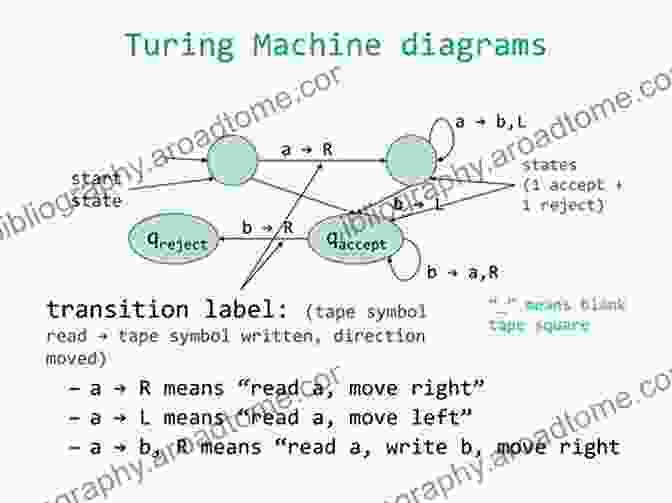
Turing Machines
Turing machines are the most powerful automata and are capable of simulating any computation that can be carried out by a computer. They consist of a tape, a read/write head, and a finite set of states, and they operate by reading, writing, and moving the head on the tape. Turing machines serve as an abstract model for computation and form the theoretical foundation for modern computers and programming languages.
Formal Languages
Formal languages provide a precise and mathematical way to describe the structure and syntax of languages. They are used in a wide range of applications, including programming languages, compilers, and natural language processing.
Regular Languages
Regular languages are languages that can be recognized by finite automata. They are defined by regular expressions, which provide a concise and powerful way to describe patterns in strings. Regular languages find applications in text processing, pattern matching, and lexical analysis.
Context-Free Languages
Context-free languages are languages that can be recognized by pushdown automata. They are defined by context-free grammars, which specify a set of rules for generating strings in the language. Context-free languages are used in programming languages, compilers, and XML processing.
Context-Sensitive Languages
Context-sensitive languages are languages that can be recognized by linear bounded automata, a variant of pushdown automata with restricted memory capacity. They are more powerful than context-free languages and are used in natural language processing and parsing.
Computability and Complexity
Computability and complexity theory explore the fundamental limits and capabilities of computation. They seek to answer questions about what problems can be solved by computers and how efficiently they can be solved.
Computability Theory
Computability theory investigates the limits of computation and defines what problems are inherently unsolvable by computers. It introduces the concept of the halting problem and explores undecidable problems, such as the Turing halting problem, which asks whether a given program will halt or run forever.
Complexity Theory
Complexity theory classifies computational problems based on their resource requirements, such as time and space. It defines complexity classes, such as P, NP, and NP-complete, and investigates the relationships between these classes. Complexity theory has practical implications for algorithm design and optimization, helping to identify problems that are inherently difficult to solve.
Algorithms
Algorithms are precise and unambiguous instructions for performing specific tasks. They are the building blocks of computer programs and play a critical role in solving computational problems efficiently.
Types of Algorithms
There are numerous types of algorithms, each designed for specific tasks. Some common types include:
- Sorting algorithms (e.g., quicksort, mergesort)
- Searching algorithms (e.g., binary search, depth-first search)
- Graph algorithms (e.g., Dijkstra's algorithm, Kruskal's algorithm)
- Dynamic programming algorithms (e.g., longest common subsequence, knapsack problem)
- Machine learning algorithms (e.g., k-nearest neighbors, support vector machines)
Algorithm Analysis
Algorithm analysis evaluates the performance of algorithms and determines their time and space complexity. It helps to identify the most efficient algorithms for specific problems and optimize their implementation.
Discrete Mathematics
Discrete mathematics provides the mathematical foundation for theoretical computer science. It deals with discrete structures, such as sets, relations, graphs, and trees, and provides tools for analyzing and modeling computational problems.
Set Theory
Set theory provides a framework for representing and manipulating collections of objects. It introduces concepts such as unions, intersections, and complements, and is essential for understanding more complex structures like relations and graphs.
Relations and Functions
Relations and functions are used to describe connections between elements in sets. Relations model binary relationships, while functions associate each element in one set with a unique element in another set. These concepts are fundamental in data structures and database systems.
Graphs and Trees
Graphs and trees are mathematical structures used to represent hierarchical relationships. Graphs consist of nodes connected by edges, while trees are acyclic graphs with a single root node. They have applications in network modeling, data structures, and artificial intelligence.
Theoretical computer science provides a deep understanding of the foundations of computation and information. By exploring the topics covered in this guide, you will gain a comprehensive knowledge of automata theory, formal languages, computability, complexity, algorithms, and discrete mathematics. This knowledge will empower you to design and analyze algorithms, understand the limitations of computation, and contribute to the advancement of computer science and related fields.
Whether you are a student pursuing a degree in computer science, a researcher delving into the depths of computation theory, or a practitioner seeking to optimize your software development process, this guide will serve as an invaluable resource for expanding your knowledge and unlocking the secrets of theoretical computer science.
5 out of 5
| Language | : | English |
| File size | : | 14553 KB |
| Text-to-Speech | : | Enabled |
| Enhanced typesetting | : | Enabled |
| Screen Reader | : | Supported |
| Print length | : | 192 pages |
Do you want to contribute by writing guest posts on this blog?
Please contact us and send us a resume of previous articles that you have written.
 Book
Book Novel
Novel Page
Page Chapter
Chapter Text
Text Story
Story Genre
Genre Reader
Reader Library
Library Paperback
Paperback E-book
E-book Magazine
Magazine Newspaper
Newspaper Paragraph
Paragraph Sentence
Sentence Bookmark
Bookmark Shelf
Shelf Glossary
Glossary Bibliography
Bibliography Foreword
Foreword Preface
Preface Synopsis
Synopsis Annotation
Annotation Footnote
Footnote Manuscript
Manuscript Scroll
Scroll Codex
Codex Tome
Tome Bestseller
Bestseller Classics
Classics Library card
Library card Narrative
Narrative Biography
Biography Autobiography
Autobiography Memoir
Memoir Reference
Reference Encyclopedia
Encyclopedia Felicity Young
Felicity Young Faith Javane
Faith Javane Enlightened Anonymous
Enlightened Anonymous Maura Thomas
Maura Thomas Mark Johanson
Mark Johanson Rick Browne
Rick Browne Laurie A Loevner
Laurie A Loevner Erik Hanchett
Erik Hanchett Fabio Benzi
Fabio Benzi Emmeline Pankhurst
Emmeline Pankhurst Emma Carlson Berne
Emma Carlson Berne Suzanne Finstad
Suzanne Finstad Rafael Medoff
Rafael Medoff Flo Gnan
Flo Gnan Emily Cooper
Emily Cooper Greg Critser
Greg Critser William Preston Vaughn
William Preston Vaughn Smith Wigglesworth
Smith Wigglesworth Eric Wareheim
Eric Wareheim Felix Wemheuer
Felix Wemheuer
Light bulbAdvertise smarter! Our strategic ad space ensures maximum exposure. Reserve your spot today!
 Jerome BlairFollow ·8.1k
Jerome BlairFollow ·8.1k Russell MitchellFollow ·9.2k
Russell MitchellFollow ·9.2k Jared PowellFollow ·9k
Jared PowellFollow ·9k Chinua AchebeFollow ·17k
Chinua AchebeFollow ·17k T.S. EliotFollow ·14k
T.S. EliotFollow ·14k Matt ReedFollow ·17.4k
Matt ReedFollow ·17.4k Jace MitchellFollow ·19.4k
Jace MitchellFollow ·19.4k Hugh ReedFollow ·18.5k
Hugh ReedFollow ·18.5k

 Troy Simmons
Troy SimmonsStories From The Life Of Baha: A Must-Read For Spiritual...
Discover the Inspiring Teachings and Enriching...

 Wesley Reed
Wesley ReedDuke Review of MRI Principles: Case Review - Your Gateway...
Unveiling the Essence...

 Ralph Waldo Emerson
Ralph Waldo EmersonThe Big Book of NFTs: Your Ultimate Guide to the Digital...
In the rapidly evolving world of digital...

 Jason Hayes
Jason HayesUnveiling the Labyrinth: The Cheat Sheet Novel and its...
In the realm...
5 out of 5
| Language | : | English |
| File size | : | 14553 KB |
| Text-to-Speech | : | Enabled |
| Enhanced typesetting | : | Enabled |
| Screen Reader | : | Supported |
| Print length | : | 192 pages |